linkPath Tracing
linkProblem Statement
Perform a theoretical investigation of some visibility algorithm or global illumination method.
linkBackground
Path Tracing was the first general-purpose unbiased Monte Carlo light transport algorithm introduced by Kajiya in 1986 that is used in graphics. It is similar to ray tracing in which rays are cast from a virtual camera and traced through a simulated scene. the light rays are reduced by a BRDF (Bidirectional Reflectance Distribution Function) to define how much of it will go towards the camera. This step is repeated for each pixel in the final image.
Path tracing uses random sampling to incrementally compute a final image. The random sampling process makes it possible to render some complex phenomena which are not handled in regular ray tracing, but it generally takes longer time to produce a high quality path traced image. The random sampling in path tracing causes noise to appear in the rendered image. The noise is removed by letting the algorithm generate more samples, i.e. color values resulting from a single ray. Unlike other methods, path tracing replicate real behaviours than other alternatives don't integrate natively like blur, ambient occlusion, depth of field and shadows.

linkSamples Per Pixel (SPP)
The number of samples per pixel (SPP) is the defining factor for render quality. The higher SPP in a rendered image the less noise will be noticeable. However the added quality per sample decreases the more samples you have already (since each sample is just contributing to an average over all samples). The difference in image quality between, for instance, 20,000 SSP and 21,000 SSP will not be as noticeable as between 1,000 SSP and 2,000 SSP.
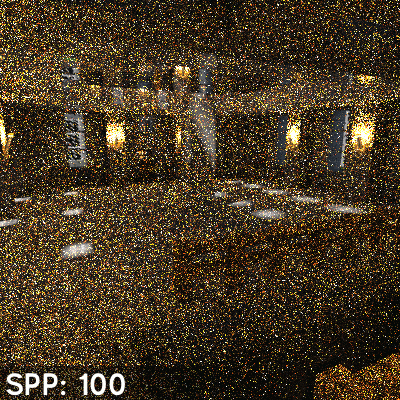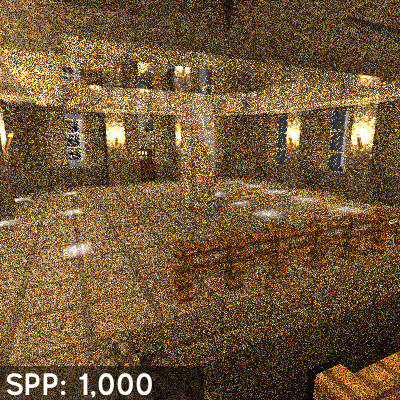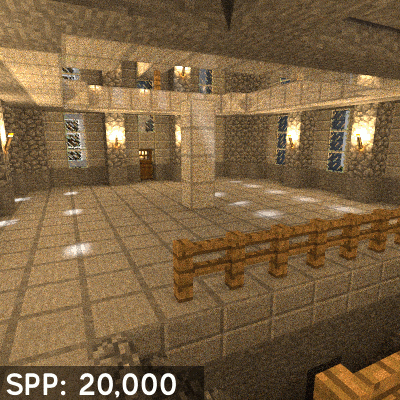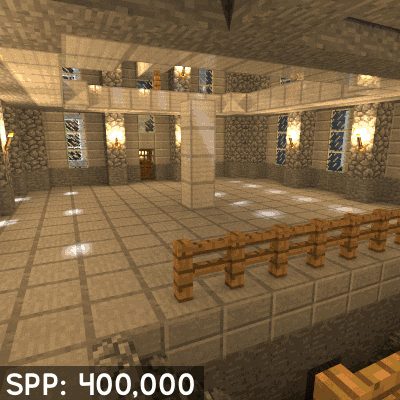
linkGlobal Illumination
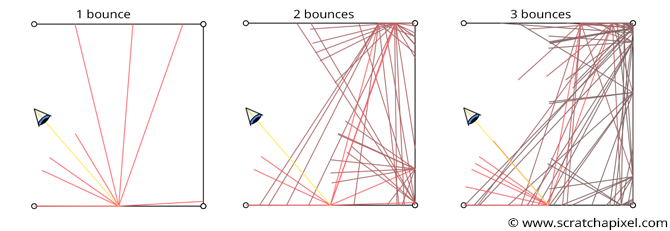
we see things because light emitted by light sources such as the sun bounces off of the surface of objects. When light rays bounce only once from the surface of an object to reach the eye, we speak of direct illumination. But when light rays are emitted by a light source, they can bounce off of the surface of objects multiple times before reaching the eye. This is what we call indirect illumination because light rays follow complex paths before entering the eye.
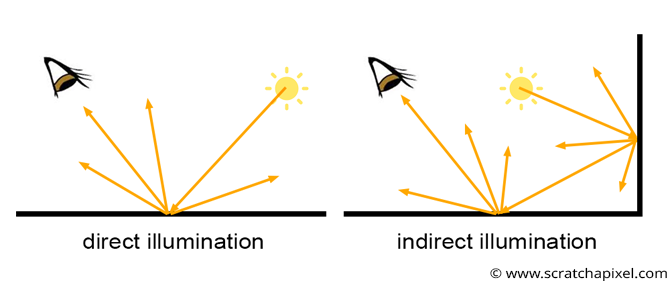
linkBackward Tracing
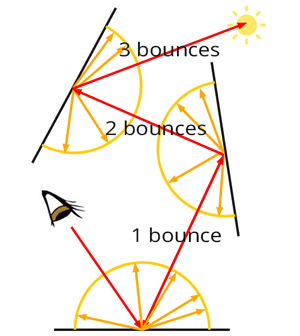
It is hard to come with a generic solution that solves all light paths: light rays can interact with many different kind of materials before entering the eye. As you know, in the real world, light travels from light sources to the eye. Simulating the path of a light ray as it interacts with various materials is thus something that we can easily do with a computer. Though the problem is that forward tracing in computer graphics is not an efficient way of making up an image. For this reason is prefered Backward Tracing which consists of tracing the path of light rays from the eye, back to the light source where they originated from.
linkIndirect Lighting
Light illuminating a given point P on the surface of an object, can come from all possible directions contained within a hemisphere oriented about the surface normal N at P. When dealing with direct light sources, finding where light comes from is simple. We just need to loop over all the light sources contained in the scene and either consider their direction if it is a directional light or trace a line from the light source to P if the light is a spherical or point light source.
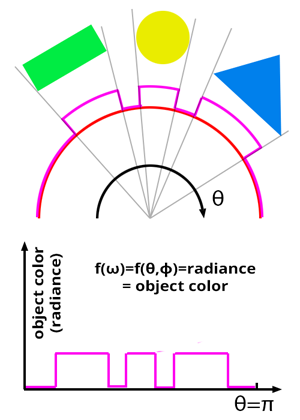
Though when we want to account for indirect lighting, every surface above P may redirect light towards P. Though,finding the direction of light rays when you deal with delta lights is simple but how do we do that when light is emitted by a surface? There is no unique point light position from which the light direction can be computed. A simple aproximation to deal with this problem is the Monte Carlo Integration. For this situation the algorithm gather all light come from all possible directions above the hempisphere oriented about the normal at P. It is represented with the next integral:
gather light=∫ΩLi. Gather Light≈1N∑n=0N castRay(P, randomDirectonAboveP) .
It is based on the idea that you can approximate or estimate how much light is redirected towards P by other objects in the scene, by casting rays from P in random directions above the surface and evaluating the color of the objects these rays intersect. The "quality" of this approximation mostly depends on N, the number of samples used. The higher N, the more likely you are to get a result close to the actual result of this integral.
Remember that what we want, is to collect all light reflected towards P by objects in the scene, which we can write with the integral described before. The variable Ω here, represents the hemisphere of directions oriented around the normal at P. This is the equation we are trying to solve and to get an approximation of this integral using Monte Carlo integration, we need to "sample" the function on the right side of the integral sign (the ∫ symbol), the Li term.
linkSampling
Since we need to account for the fact that light can come from anywhere above P, what we do instead in the case of Monte Carlo integration, is to select some random directions within the hemisphere oriented about P and trace rays in these directions into the scene. If these rays intersect some geometry in the scene, we then compute the object color at the intersected point which we assume to be the amount of light that the intersected object reflects towards P along the direction defined by the ray.
linkAlgorithm
linkStep 1
Select a random location in the half disk of the unit circle which we can do by simply drawing a random value for the angle θ anywhere in the range [0,π].
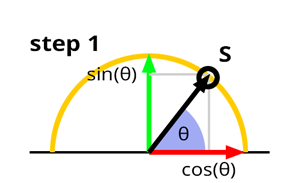
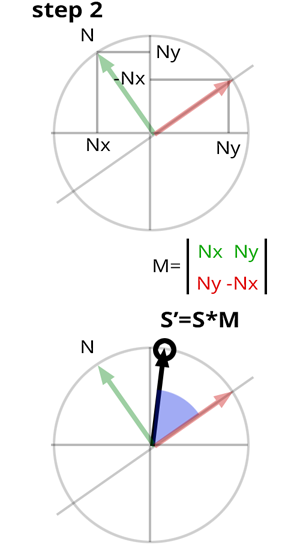
linkStep 2
Construct a 2x2 matrix using the shaded point normal and an interesting property of 2D vectors: a 2D cartesian coordinate system can be created from (Vx,Vy) and from (Vy,−Vx)
linkStep 3
Trace a ray in the sampled direction to find out if the ray that we just sampled hits an object in the scene. If it does, we then compute the color at the point of intersection which we assume to be the amount of light the intersected object reflects towards P along the ray direction.
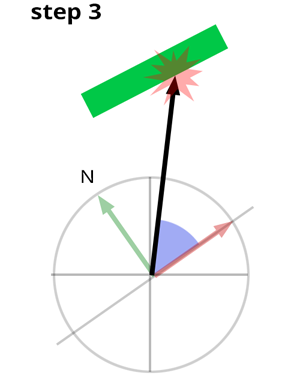
linkStep 4
Multiply the object color at the ray intersection point by the cosine of the angle between the surface normal N and the light direction
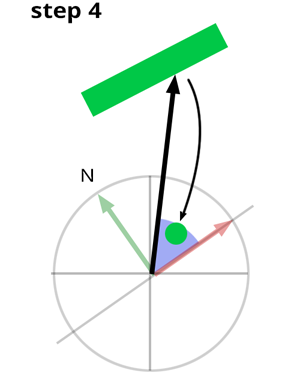
linkStep 5
Accumulate the contribution of the sample.
linkStep 6
The Monte Carlo integration equation tells us we need to divide the sum of the samples contribution by the sample size, the number N.
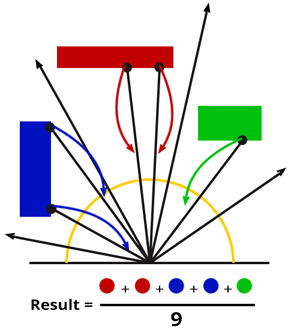
linkStep 7
accumulate the diffuse color of the object at P due to direct and indirect illumination and multiply the sum of these two values by the object.
linkReferences
- http://www.graphics.stanford.edu/courses/cs348b-01/course29.hanrahan.pdf
- https://www.online-tech-tips.com/computer-tips/what-is-path-tracing-and-ray-tracing-and-why-do-they-improve-graphics/
- https://www.pbr-book.org/3ed-2018/Light_Transport_I_Surface_Reflection/Path_Tracing
- https://chunky.llbit.se/path_tracing.html